About UAQ - University of L'Aquila, Italy
UAQCoordinator

University of L'Aquila (UAQ) Italy
UAQDeputyCoordinator

University of L'Aquila (UAQ) Italy
Semester #1 Cohort #2025 @ UAQ
Foundations of Applied Mathematics;
ECTS Credits: 9 | Semester: 1 | Year: 1 | Campus: University of L'Aquila | Language: English | Code: DT0626
Unit Coordinator: Marco Di Francesco, Michele Palladino
Aims:
Introducing basic tools of advanced real analysis such as metric spaces, Banach spaces, Hilbert spaces, bounded operators, weak convergences, compact operators, weak and strong compactness in metric spaces, spectral theory, in order to allow the student to formulate and solve linear ordinary differential equations partial differential equations, classical variational problems, and numerical approximation problems in an "abstract" form. Provide a primer of abstract measure and integration to be used in advanced probability and analysis courses.
Content:
Pre-requisites:
Basic calculus and analysis in several variables, linear algebra.
Reading list:
The first semester at UAQ is common to all students. It provides a sound background in applied mathematics based on advanced theoretical subjects such as functional analysis, applied partial differential equations, dynamical systems, continuum mechanics, and control systems.
This semester prepares the students to perform simulations in diverse modelling frameworks, as well as to successfully tackle subjects in semester 2 such as advanced numerical calculus, optimization, and stochastic calculus. To perform this task, Semester 1 courses provide a systematic approach to the formulation of applied problems in interdisciplinary fields, and a rigorous approach to mathematical modelling. More precisely, students in this semester are provided “exact” resolution methods for (ordinary and partial) differential equations, the “infinite dimensional” approach of functional analysis (needed in approximation theory, variational calculus, and numerical analysis), a modern and “engineering oriented” approach to control, and an introduction to the mathematical theory of continuum media, a subject that is touched by several specialization tracks.
Teaching staff with longstanding experience with international joint programs in applied mathematics is in charge of this semester. The University of L’Aquila features a research group in mathematical analysis combining three generations of applied mathematicians with excellent international reputation in their field and with an outstanding research record, with main focus on partial differential equations with applications to physics, engineering, social sciences, biology and medicine.
September 2025
September 2026
September 2026
Campus
Cohort
2025
Semester
ECTS Credits
Semester #3 Cohort #2025 @ UAQ
Modelling and simulation for the mitigation of natural disasters;
ECTS Credits: 9 | Semester: 1 | Year: 2 | Campus: University of L'Aquila | Language: English | Code: DT0113
Unit Coordinator: Corrado Lattanzio
Aims:
LEARNING OBJECTIVES.
The course aims at providing advanced mathematical notions used in the field of (applied) mathematical analysis and their applications to a variety of topics, including the basic equations of mathematical physics and some current research topics about linear and nonlinear partial differential equations.
Those objectives contribute to the learning goals of the entire course of studies, as the inner coherence of the master degree in Mathematics was verified at the time of the planning of the master program.
LEARNING OUTCOMES.
At the end of the course, the student should:
1. know the advanced mathematical notions used in the field of (applied) mathematical analysis, as measure theory, Sobolev Spaces, distributions, and their applications to the theory of linear and non-linear partial differential equations;
2. understand and be able to explain thesis and proofs in advanced mathematical analysis;
3. have strengthened the logic and computational skills;
4. be able to read and understand other mathematical texts on related topics.
Content:
Distributions. Locally integrable functions. The space of test function D(Ω). Distributions associated to locally integrable functions. Singular distributions. Examples. Operations on distributions: sum, products times functions, change of variables, restrictions, tensor product. Differentiation and his properties; comparison with classical derivatives. Differentiation of jump functions. Partition of unity. Support of a distribution; compactly supported distributions. Fourier transform and tempered distributions. Convolution between distributions and regularization of distributions. Denseness of D(Ω) in D′(Ω). Sobolev spaces. Definition of weak derivatives and his motivation. Sobolev spaces Wk,p(Ω) and their properties. Interior and global approximation by smooth functions. Extensions. Traces. Embeddings theorems: Gagliardo–Nirenberg–Sobolev inequality and embedding theorem for p < n. Hölder spaces. Morrey inequality. Embedding theorem for p > n. Sobolev inequalities in the general case. Compact embeddings: Rellich–Kondrachov theorem, Poincaré inequalities. Embedding theorem for p = n. Characterization of the dual space H-1. Second order parabolic equations. Definition of parabolic operator. Weak solutions for linear parabolic equations. Existence of weak solutions: Galerkin approximation, construction of approximating solutions, energy estimates, existence and uniqueness of solutions. First order nonlinear hyperbolic equations. Scalar conservation laws: derivation, examples. Weak solutions, Rankine-Hugoniot conditions, entropy conditions. L1 stability, uniqueness and comparison for weak entropy solutions. Convergence of the vanishing viscosity and existence of the weak, entropy solution. Riemann problem. Measures. System of sets, Positive Measures, Outer Measures, Construction of Measures, Signed Measures, Borel and Radon Measures
Integration. Measurable Functions, Simple Functions, Convergence Almost Everywhere, Integral of Measurable Functions, Convergences of Integrals, Fubini-Tonelli Theorems.
Differentiation. The Radon-Nikodym Theorem, Differentiation on Euclidean space, Differentiation of the real line.
Radon measures and continuous functions. Spaces of continuous functions, Riesz Theorem.
Pre-requisites:
Basic notions of functional analysis, functions of complex values, standard properties of classical solutions of semilinear first order equations, heat equation, wave equation, Laplace and Poisson's equations.
Reading list:
- L. Ambrosio, G. Da Prato, A. Mennucci. Introduction to measure theory and integration. Edizioni della Normale. - L. Ambrosio, N. Fusco, D. Pallara. Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. - V.I. Bogachev. Measure theory, Volume I, Springer. - H. Brezis. Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext, Springer. - P. Cannarsa, T. D’Aprile. Introduction to Measure Theory and Functional Analysis. Springer. - C.M. Dafermos. Hyperbolic Conservation Laws in Continuum Physics, Springer. - L.C. Evans. Partial Differential Equations. Graduate Studies in Mathematics, Vol. 19, AMS. - L. Evans, R. Gariepy. Measure Theory and Fine Properties of Functions, CRC Press. Revised Edition. - G.B. Folland. Real analysis: Modern techniques and their applications. New York Wiley - G. Gilardi. Analisi 3. McGraw–Hill. - L. Grafakos, Classical Fourier Analysis. Springer. - V.S. Vladimirov. Equations of Mathematical Physics. Marcel Dekker, Inc
This path brings together various contexts in which mathematical modelling can study, prevent, and possibly mitigate the occurrence of natural disasters of various types, such as floods, landslides, earthquakes, tidal waves, hurricanes, and forest wildfires. More and more such events (especially floods and fires) affect the EU environment, so that more and more of the data collected can be studied in a mathematical context.
This has led to the recent formulation of predictive models using transport partial derivative equations, machine learning and artificial intelligence, and the study of risk assessment models. In the case of earthquakes, there is a strong intersection with elastic media modelling, a branch of continuum dynamics. Part of the curriculum is based on analytical methods.
Therefore, the “Advanced Analysis” unit is also offered in this specialisation to support the methodological part of the “Mathematical Fluid Dynamics” unit, taught by Prof. Donatella Donatelli, a world-class expert in the field. The “Mathematical Modelling and HPC Simulation of Natural Disasters” unit (taught by Dr Donato Pera), on the other hand, focuses on computational methods of HPC type in contexts such as wildfire and earthquake modelling, also touching on drift-diffusion models for the study of floods. Models for sedimentation and erosion are also touched upon to help improve the profiling of the seabed exposed to flooding. This part of the course makes use of the experience of the UAQ group within Spoke 5 “Envorinment and Natural Disasters” of the “Italian Research Center on High Performance Computing, Big Data and Quantum Computing”, of which Prof Rubino, Di Francesco and Fagioli are members, and of which Dr Donato Pera is the principal researcher in the numerical simulation part. The “Artificial Intelligence and Machine Learning for Natural Hazards Risk Assessment” unit, taught by Dr Federica Di Michele of the National Institute of Geophysics and Volcanology (INGV), deals with the artificial intelligence-based approach to all these problems, and is more dedicated to the analysis of risks associated with the various extreme events of interest. Finally, the Application Driven Unit “Numerical modelling and application to water-related natural hazards”, coordinated by an engineer from the field of hydraulics (Prof. Marcello Di Risio, director of the UAQ Civil Engineering Department), provides aspects more related to the physics behind the various extreme phenomena involving water as the main actor, as well as dealing with specific numerical techniques for such models.
The main external collaborator in this specialisation is the National Institute of Geophysics and Volcanology, with which UAQ has a well-established agreement (particularly after the 2009 earthquake), but there is also an important interaction with the aforementioned Italian Research Center on HPC, Big Data and Quantum Computing.
September 2025
September 2026
September 2026
Campus
Cohort
2025
Semester
3
ECTS Credits
Semester #3 Cohort #2025 @ UAQ
Mathematical modelling for health care;
ECTS Credits: 9 | Semester: 1 | Year: 2 | Campus: University of L'Aquila | Language: English | Code: DT0113
Unit Coordinator: Corrado Lattanzio
Aims:
LEARNING OBJECTIVES.
The course aims at providing advanced mathematical notions used in the field of (applied) mathematical analysis and their applications to a variety of topics, including the basic equations of mathematical physics and some current research topics about linear and nonlinear partial differential equations.
Those objectives contribute to the learning goals of the entire course of studies, as the inner coherence of the master degree in Mathematics was verified at the time of the planning of the master program.
LEARNING OUTCOMES.
At the end of the course, the student should:
1. know the advanced mathematical notions used in the field of (applied) mathematical analysis, as measure theory, Sobolev Spaces, distributions, and their applications to the theory of linear and non-linear partial differential equations;
2. understand and be able to explain thesis and proofs in advanced mathematical analysis;
3. have strengthened the logic and computational skills;
4. be able to read and understand other mathematical texts on related topics.
Content:
Distributions. Locally integrable functions. The space of test function D(Ω). Distributions associated to locally integrable functions. Singular distributions. Examples. Operations on distributions: sum, products times functions, change of variables, restrictions, tensor product. Differentiation and his properties; comparison with classical derivatives. Differentiation of jump functions. Partition of unity. Support of a distribution; compactly supported distributions. Fourier transform and tempered distributions. Convolution between distributions and regularization of distributions. Denseness of D(Ω) in D′(Ω). Sobolev spaces. Definition of weak derivatives and his motivation. Sobolev spaces Wk,p(Ω) and their properties. Interior and global approximation by smooth functions. Extensions. Traces. Embeddings theorems: Gagliardo–Nirenberg–Sobolev inequality and embedding theorem for p < n. Hölder spaces. Morrey inequality. Embedding theorem for p > n. Sobolev inequalities in the general case. Compact embeddings: Rellich–Kondrachov theorem, Poincaré inequalities. Embedding theorem for p = n. Characterization of the dual space H-1. Second order parabolic equations. Definition of parabolic operator. Weak solutions for linear parabolic equations. Existence of weak solutions: Galerkin approximation, construction of approximating solutions, energy estimates, existence and uniqueness of solutions. First order nonlinear hyperbolic equations. Scalar conservation laws: derivation, examples. Weak solutions, Rankine-Hugoniot conditions, entropy conditions. L1 stability, uniqueness and comparison for weak entropy solutions. Convergence of the vanishing viscosity and existence of the weak, entropy solution. Riemann problem. Measures. System of sets, Positive Measures, Outer Measures, Construction of Measures, Signed Measures, Borel and Radon Measures
Integration. Measurable Functions, Simple Functions, Convergence Almost Everywhere, Integral of Measurable Functions, Convergences of Integrals, Fubini-Tonelli Theorems.
Differentiation. The Radon-Nikodym Theorem, Differentiation on Euclidean space, Differentiation of the real line.
Radon measures and continuous functions. Spaces of continuous functions, Riesz Theorem.
Pre-requisites:
Basic notions of functional analysis, functions of complex values, standard properties of classical solutions of semilinear first order equations, heat equation, wave equation, Laplace and Poisson's equations.
Reading list:
- L. Ambrosio, G. Da Prato, A. Mennucci. Introduction to measure theory and integration. Edizioni della Normale. - L. Ambrosio, N. Fusco, D. Pallara. Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. - V.I. Bogachev. Measure theory, Volume I, Springer. - H. Brezis. Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext, Springer. - P. Cannarsa, T. D’Aprile. Introduction to Measure Theory and Functional Analysis. Springer. - C.M. Dafermos. Hyperbolic Conservation Laws in Continuum Physics, Springer. - L.C. Evans. Partial Differential Equations. Graduate Studies in Mathematics, Vol. 19, AMS. - L. Evans, R. Gariepy. Measure Theory and Fine Properties of Functions, CRC Press. Revised Edition. - G.B. Folland. Real analysis: Modern techniques and their applications. New York Wiley - G. Gilardi. Analisi 3. McGraw–Hill. - L. Grafakos, Classical Fourier Analysis. Springer. - V.S. Vladimirov. Equations of Mathematical Physics. Marcel Dekker, Inc
This path aims to provide specific training in mathematical modelling applied to various contexts in health care. The consolidated experience of the UAQ group in mathematical modelling in micro-biology, as evidenced by the presence of Prof. Cristina Pignotti and Prof. Simone Fagioli (experts in biological aggregation models, chemotaxis, and mathematical physiology), allows us to provide the “Biomathematics” unit, which includes elements of pharmaco-kinetics with applications to tumour growth.
The “Mathematical modelling of multi-agent systems” unit addresses recently formulated modelling elements with applications to diagnostics, the study of the spread of epidemics, and genetics. It also provides elements of “swarm theory” with applications to the use of robotics in medicine. In this field, UAQ relies on Prof. Di Francesco and his team, which also includes the recently hired Dr Antonio Esposito, a recognised expert in graph modelling. Both these units require very advanced concepts of mathematical analysis offered in the well-established “Advanced Analysis” unit, for which we count on the expertise of Prof. Corrado Lattanzio. Prof. Raffaele D'Ambrosio brings his leading role in numerical methods for stochastic models to his unit “Computational methods in health-care systems”.
As an Application Driven Unit, in this path we offer “System Biology”, which will be taught by an engineer from the field of control systems, dealing with stochastic models to describe complex chemical processes at the origin of various phenomena of interest in medicine.
This specialisation is supported by a well-established pharmaceutical industry substrate in and around L'Aquila, with which the consortium has well-established relations.
Furthermore, the University of L'Aquila recently signed a General Cultural and Scientific Cooperation Agreement with Brigham and Women's Hospital in Boston (BWH. a teaching hospital of Harvard Medical School and the largest hospital in the Longwood Medical Area in Boston). This partnership was enhanced by the recent affiliation of UnivAq to the “Network Medicine Alliance” (see https://www.network-medicine.org/). The team led by Prof. Joseph Loscalzo (Distinguished Chair in Medicine at Harvard Medical School) at BWH acts as overseas partner of InterMaths and contributes by offering computational theses project opportunities (1-2 per year) in biomedicine in which the students can gain experience.
September 2025
September 2026
September 2026
Campus
Cohort
2025
Semester
3
ECTS Credits
Practical information for your semester in L'Aquila
Academic Calendar & Term dates
Key Dates | 2025/2026 academic year |
|---|---|
Semester 1 | 22 September - 9 January (PDF Schedule) |
Christmas vacation | 23 December - 6 January |
Semester 1 examinations | 12 January - 22 February |
Semester 2 | March - SeptemberTUHH Semester2 starts with some preliminary activities run in L'Aquila in March, then continues in Hamburg as of April 1. |
Holidays (Italy) | 1 November, 8 December, 6 April, 25 April, 1 May, 2 June, 10 June, 15 August |
Visa information
Applying for an Italian study visa
Non-EU students selected to study at the University of L'Aquila will need to apply for a student visa at the nearest Italian Embassy/Consulate. The visa application requirements and processing time can be lengthy, taking anywhere from a few weeks up to several months. It is very important that you contact the nearest Italian Embassy for information as early as possible.
Please notice that, before joining our programmes, you will only need to apply for one visa only at an Italian Embassy/Consulate, as Italy is the location for your first semester/year. Afterwards, while you're spending your semester(s) in Italy, you will have the chance to apply for another visa or residence permit, e.g. a German one if you're spending your Semester 2 in Hamburg, at the German Consulate based in Rome.
Web-based visa application on Universitaly.it
The visa application procedure is completely web-based. All non-EU students not living in Italy are requested to pre-enrol using the online platform called UNIVERSITALY. Once your pre-enrolment request on Universitaly.it has been approved by the University of L'Aquila, you will receive a confirmation email. After that, you will have to get in contact with the local Italian Diplomatic-consular mission for the visa request process. Please note that the university confirmation email does not automatically imply the issue of a study visa for you, which is all up to the Diplomatic mission you're in contact with, instead.
Documents required
Please get in contact with the local embassy/consulate to learn more about the specific requirements they might have in that region.
Recognition of Qualifications
To complete your visa application first and finalize your enrolment after reaching L'Aquila, you'll have to submit verification of your previous university qualifications
Residence Permit
If you need a visa to stay in Italy, remember that you will also have to apply for an Italian residence permit within 8 days of arriving in our country.
Italian Residence Permit
The InterMaths team will assist you with preparing all the required documentation, which includes a couple of forms to be filled in and, among others:
A full copy of your passport (every single page, cover included)
A copy of your health insurance card
Accommodation proof
A temporary one from a hotel/B&B will also work (you may submit proof of your permanent accommodation at a later stage when visiting the Immigration Office)
Financial proof
Enrolment certificate
All you need to do is visit an Italian post office and withdraw the required form known as "kit permesso di soggiorno" ("soggiorno" sounds like "sojjorno"). Then, bring it to campus and we'll fill it in together!
After that, put all the required documents (including blank forms) back in the envelope, visit an Italian post office once again and complete the submission process (including payment of the required fees) with the post office clerks. After that, your application will be submitted to the L'Aquila Ufficio Immigrazione ("questura" in Italian, which sounds like "kuestura") via the post office itself.
At the end of the submission process, the clerk at the post office will hand you out three receipts, which will be considered as your temporary residence permit (always carry a copy with you whenever you're around and drop one off at our Registrar's Office to confirm your enrolment).
On such receipts, you'll also find the date and time of the appointment fixed for you at the L'Aquila police station (Questura, Ufficio Immigrazione) to complete the rest of the required procedures, which includes an interview for fingerprints (carry your passport & 4 ID-size photos). Eventually, you'll be summoned for another appointment to collect your final (plastic) permit card - the one you can see on this page.
The whole process will be complete in approximately 2 months (but it might even take longer) and will cost you around 120 euros.
Enrolment procedure
After getting to L'Aquila, you'll have to complete your enrolment at the University of L'Aquila, which is the coordinating institution of your MSc programme.
The enrolment process involves a preliminary online phase to be performed on our university info system "Segreteria Virtuale", which is usually taken care of by the InterMaths consortium.
The process consists of:
Account registration
Online pre-enrolment (it has nothing to do with the Pre-Enrolment on Universitaly.it to get a study visa)
Fee payment.
Afterwards, to finalize your online enrolment, you'll have to submit:
Qualifications (i.e., transcript and degree certificate) from your university of origin in their original format.
Verification of your previous university qualifications. To do so, you'll have to submit ONE of the following certificates:
CIMEA Statements of comparability
CIMEA (ENIC/NARIC network) has implemented a service of certification and comparison of Italian and foreign qualifications - note that you'll only need to request a statement of comparability.
Apply here
Declaration of Value (DoV)
The DoV is a document providing an official description of your academic certificates, duly legalized by the Consular office of the Italian Embassy in the country where such a degree was gained.
Diploma Supplement
Direct Verification via UAQ
Starting this year (2024 edition) you may entitle the University of L'Aquila to contact the institution where you obtained your previous degree and verify the genuine nature of your qualifications. Further information about this procedure will be emailed to you by our staff.
Note that some local Diplomatic-consular missions might still require you to obtain a Declaration of Value (DoV) or a CIMEA statement before they issue your study visa, even though they know that our university accepts other types of verification (any of the 4 listed above).
If that is the case, you will have to go through the DoV/CIMEA request process, otherwise, you will never obtain any visa from that specific embassy. Please check in good time in advance the particular requirements in force at the Diplomatic-consular you're about to visit for your visa.
For further information on this topic, check out the related webpage on the UAQ site: www.univaq.it/international
Health & Travel Insurance
AON 24/7 emergency assistance
Dial: +31104488260
Contact form (non-emergency cases): link
Find the nearest open pharmacy in L'Aquila
Waitaly (Generali) 24/7 emergency assistance
Dial: 800450130 (toll-free from Italian phones only)
+39 0258286788 (any other phones)
Doctor-on-call (Guardia medica)
Out-of-hours (on call) doctor.
Address: Ex ONPI, via Capo Croce 1 ("Torrione" neighbourhood).
Available Mon-Fri from 8pm till 8 am, and from 10 am on Sat till 8 am on the following Mon.
Psychological support
All our students (either non-EU or EU) must hold valid insurance covering risks related to health, accidents, death, permanent invalidity, and civil responsibility (including travel assistance) while they are outside their home country.
An insurance card will also be necessary to apply for a residence permit.
↘ Erasmus Mundus (EMJMD) InterMaths students (either scholarship holders or not)
Before their arrival, they will receive free of charge an insurance card covering risks related to health, accidents, death, permanent invalidity, and civil responsibility, as per the minimum requirements set out by EACEA
↘ Other students (enrolled in the RealMaths or MathMods programs).
Non-European students must ensure they hold valid insurance to obtain a visa, a residence permit, and enrolment at university. Requirements may vary a lot from country to country even within the Schengen area. Generally speaking, such insurance must offer coverage of medical costs for min. 30,000 EUR, as well as risks related to health, accidents, permanent invalidity, urgent health attention and/or emergency hospital treatment or even death, including possible repatriation for medical reasons.
EU students, on the other hand, won't need to purchase any additional private insurance if they don't think they need one, as long as they hold a valid European Health Insurance Card (EHIC).
Though you may get an Italian residence permit even by providing cheap insurance coverage, we encourage everybody to ensure that the insurance you are about to purchase is as comprehensive as possible.
Note that some of the options listed below, though officially valid throughout the Schengen area, may not be sufficient to obtain a visa/permit when you are going to spend a semester in another country, in Germany or Austria for instance. Always double-check before completing your purchase for a whole year or more, and contact the related staff at our partners in advance, because in other countries than Italy, they might require that you purchase a more comprehensive one and/or even public health insurance to obtain a visa/permit and even to seek enrolment at their university.
All the below-listed companies offer insurance that complies with the minimum requirements to obtain an Italian residence permit. Once again, though they are all officially valid within the Schengen area, they might not be enough to obtain a visa/residence/enrolment in other countries than Italy.
AON
[AON 24/7 emergency assistance: # +31 (0)10 44 88 260]Protrip-World by DrWalter
Waitaly This is the cheapest option (direct link) in Italy. However, note that it is not EACEA compliant (thus, not valid for Erasmus Mundus programs), but it is still valid to obtain an Italian residence permit to attend other programmes, like RealMaths for instance.
[Waitaly 24/7 emergency assistance via Generali 800 450 130 (toll free from Italian phones only) or +39 02 582 867 88]
Accommodation options in L'Aquila
Student's halls of residence
In Italy, students' halls of residence (including other facilities for students like cafeterias, gyms etc) are not managed by universities. The public body in charge of them is, in our case, the Abruzzo Regional Agency for Education, aka A.D.S.U. (Azienda per il Diritto agli Studi Universitari - L'Aquila).
If you wish to find a place in the dorms and shared flats managed by A.D.S.U., (this year, the student's flats are the ones in the block called "Il Moro" at a 20-minute walk from our campus, see Google Maps) you will have to apply typically in the second half of August. But note that:
Places are limited and usually reserved for students from low-income families.
Ranking lists might be published even in late October, which means you will be spending a lot for a temporary place to stay (e.g. bed and breakfast) in your first weeks in L'Aquila while you are waiting for the lists to be out.
Private halls
Lately, a new student hall has opened up in town - it's known as Camplus. It is a private one, with no relation whatsoever with our university, but it is ideally located in the heart of the city centre, it can be booked online in advance, and their fares include Wi-Fi, cleaning, maintenance etc. What's more, it is possibly the only one in town offering accommodation for a semester only (most other places will expect you to sign a one-year contract instead).
Check out their website to submit your application and find out more.
Private shared flats
As L'Aquila is undergoing huge reconstruction after the 2009 earthquake, we strongly suggest you opt for renting a flat from private owners. The cost per person ranges from 200 to 350 euros per month depending on several factors, e.g. shared or private rooms, utility bills included or not, and neighbourhood. By the way, living near the campus (the area is in a suburb in west L'Aquila known as Coppito) can be cheaper, but this means living away from the city life (events, nightlife, restaurants...).

Please make contact with Aquilasmus - ESN L'Aquila to receive support from a buddy with finding a place to stay in L'Aquila. Just so you know, support is provided free of charge by volunteers and only starts within 2 weeks after your arrival in L'Aquila (weekends not included).
Camplus is a newly-established hall of residence located right in L'Aquila city centre. It includes single and double ensuites, maintenance, wifi, cleaning, utilities etc. Check out the current selection announcement for more details and the applicaion form.
Accommodation options in L'Aquila
Your Aquilasmus buddy will typically meet you within two weeks (excluding weekends) after your arrival to help you find a place (note that they can't offer any kind of support before you get to L'Aquila). For your first days in L'Aquila, you may refer to the links below
ADSU Hall of Residence
ADSU (Abruzzo regional agency for education)
Adverts on Univaq.it
airbnb
Vacation rentals in L'Aquila
Idealista.it
FB group
"Cerco/Affitto Casa a L'Aquila!"
Bed & Breakfast in L'Aquila
Vacation rentals in L'Aquila
Periscopio
ADs listing on L'Aquila local newspaper
How to get to L'Aquila
Rome Fiumicino
Rome Ciampino
Both airports are connected to L'Aquila by express coach service operated by Gaspari or Flixbus. Read the section below ("By Bus") for further information.
Additional coach services (operated by T.U.A. and Itabus) are available from the "Tiburtina train station" (Stazione Tiburtina) located in East Rome. But that means you'll have to first get on a train/bus/undeground from the airport to get to the "Tiburtina train station", which will take you one hour or so, at least. So, we strongly suggest you use the other option above, as those coaches will be departing right from inside the aiport parking area.
Lastly, be informed that a bunch of European cities are also connected to the Abruzzo Airport in Pescara, located at about 100 km to the east of L'Aquila.
Getting to campus
Our programmes are coordinated and hosted by D.I.S.I.M. (Department of Information Engineering, Computer Science, and Mathematics) located on the Coppito campus in via Vetoio - West L'Aquila.
The Coppito campus also hosts other faculties: biology, chemistry, physics and, most importantly, the main city hospital ("ospedale" in Italian). Keep that in mind whenever you ask for directions, as everybody knows where the main hospital (ospedale) is.
Then, the University of L'Aquila is made up of several other campuses spread over the whole city, each of which has its own focus and identity. To get an overview, check out this interactive map.
Bus routes
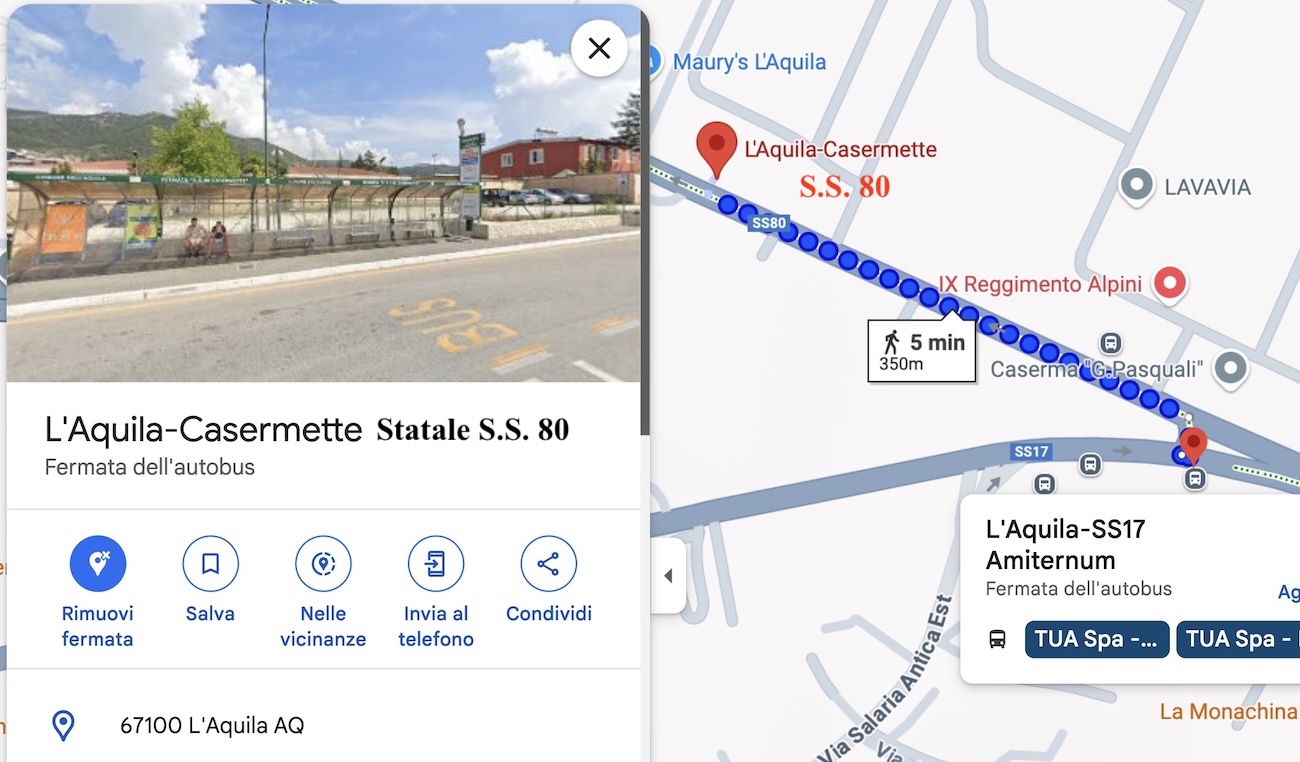
There are two bus terminals:
A small one in west L'Aquila (generally referred to as "Hotel Amiternum", "Motel Agip" by locals or "Strada Statale S.S. 17"), which is actually a stall, but it's the spot where most Flixbuses, Gaspari buses or others from Rome, Fiumicino airports and other nearby towns will stop (for both alighting and boarding).
The actual Terminal in east L'Aquila (aka "Collemaggio" by locals because of the nearby Basilica, or more officially "Lorenzo Natali"), close to the historical centre.
Both websites are only in Italian, but all you need to do is enter the word "ospedale" or "Università - Polo Coppito" or "L'Aquila Ospedale Università" in the search box (indirizzo di arrivo).
Number 1 or 2U buses are very likely the AMA buses you'll need most, as they connect our campus to the bus station at the My Suites Hotel (aka Hotel Amiternum), the "L'Aquilone" shopping centre, as well as the main bus station (known as Collemaggio or Terminal) in the old city centre.
As bus routes are not available on Google Maps yet, we recommend
Travel Links
About L'Aquila
The City of L'Aquila in brief
- Reasonable cost of living
- A town of artistic interest
- Safe and quiet but also a lively university town
- Direct buses to Rome in little more than 1 hour
- Three popular ski resorts nearby as well as three national parks
- Sandy beaches at a short distance
L'Aquila is an Italian city with about 70,000 inhabitants and around 20,000 university students. It is the capital of the Abruzzo region and it is conveniently located 100 km (62 miles) east of Rome. The city is on a hill at 720 m (2365 ft) above sea level and is surrounded by mountains, most notably to the north by the Gran Sasso range, which includes the highest peaks (up to 2,900 m) of the Apennines, with several small lakes, trails and mountain climbing routes as well as deep caves. Within the province of L’Aquila there are also two national parks (Parco Nazionale Gran Sasso Monti della Laga and Parco Nazionale della Majella).
The city itself is full of history, traditions, beautiful buildings (like the Spanish Fortress) and churches (most notably, the Collemaggio Basilica). There are also a lot of good restaurants, pubs and places where students get together at night (most remarkably, on Thursdays and Saturdays). The city is also the home of L'Aquila Rugby - this team won the Italian championship five times.
For more practical and historical information about L'Aquila, click here.
Living costs
A student will spend approximately 600 euros a month:
Around 300 EUR on average for accommodation in a single room (in a twin room you may save ~50 EUR or more); note that such an amount does not usually include utilities (heating, electricity, water, Internet).
About 300 EUR to cover:
Meals (reduced fares for international students available for ~3 EUR or even free meals at the canteens in L'Aquila if you're awarded a Regional Grant).
Public transportation (a monthly bus pass in L'Aquila costs around 30 euros)
The costs for books, sports centres and other personal expenses.
University canteens and cafeterias are managed by ADSU. You will need to register by ADSU to get a digital canteen card. This will entitle you to eat at reduced fares (~3 EUR) or even get a free meal if you're awarded a Regional Grant by ADSU.
Canteen at the Math Department (Coppito campus)
Location: between the "Coppito 1 - Ricamo" and "Coppito 0 - Alan Turing" buildings, next to the University cafè.
Opening time: 12.30 pm - 2.30 pm Mon-Fri
Main university canteen
Open for lunch and dinner even at weekends
New location: via Dell'Arcivescovado 8, right in the old city centre, next to the main square Piazza Duomo
Free Time
Aquilasmus
Aquilasmus is an official student association, part of ESN (Erasmus Student Network). Aquilasmus offers several services to Erasmus students, like organizing parties, trips, international dinners, cine forums and more. Take a look at their website, join their Facebook group and check out their Instagram page to get to know other international students and be involved in their activities.
Bars, restaurants, pubs & clubs, discos
Although several buildings in the old city are still to be reconstructed after the 2009 earthquake, dozens of bars and clubs have proudly reopened their doors. You will find lots of students hanging out mostly on Thursday nights (knonw as university night) and Saturday nights. Just ask the taxi/bus driver to drop you at "Fontana Luminosa" (the big fountain near the castle) and walk into the main road "Corso Federico II". You'll see that most people gather in a small square a few steps ahead near "via Garibaldi".
Cinemas
-
Movieplex, Via Leonardo Da Vinci, Pettino, L'Aquila (25 mins walk from the Math Dept.)
Theatres
-
TSA Teatro Stabile dell'Aquila
-
Auditorium del Parco (near the Spanish fortress/castle)
Music
Excursions
Being L'Aquila ideally located in central Italy, you'll have lots of opportunities to visit Italy's top destinations: Rome, Naples, Pompei, Sicily, Florence, Venice, Verona, Milan, Turin, to mention just a few. The easiest and most convenient way to reach any of these destinations is from the bus/train stations in Rome, where you can get to by TUA/ARPA coach or Flixbus from L'Aquila (either from the bus station "Collemaggio" or from the Hotel Amiternum). Some destinations (Bologna, Venice, Verona to the North or the whole beautiful Apulia region in Southern Italy - most notably the Salento Peninsula) are more easily accessible from Pescara train station, where you can get to by TUA/ARPA coach from L'Aquila bus station or even by train (you'll have to change trains in Sulmona). Recently, most popular Italian cities have also been connected to L'Aquila by direct coaches (Flixbus).
And, if you're into art, don't miss out on the opportunity to visit Rome museums for free on the first Sunday of every month!
Short excursions around L'Aquila
Amiternum archeological site
 On the way to Pizzoli (west L'Aquila) you may stop by and visit the stunning archaeological site of Amiternum, an ancient Italic town founded by the Sabines and conquered by the Romans in the 3rd century B.C.!
On the way to Pizzoli (west L'Aquila) you may stop by and visit the stunning archaeological site of Amiternum, an ancient Italic town founded by the Sabines and conquered by the Romans in the 3rd century B.C.!
The site features an amphitheatre, a theatre, public baths as well as an aqueduct.
For more information and opening times, visit this link.
Gran Sasso and other ski resorts

If you are into skiing, there are another 2 popular ski resorts at a short distance from L'Aquila, with better facilities than Campo Imperatore:
- Campo Felice: see here
- Ovindoli: see here
Stiffe Caves (Grotte di Stiffe)

Calascio Fortress (Rocca Calascio)

https://en.wikipedia.org/wiki/Rocca_Calascio
How to get there: get to the bus station in Collemaggio (L'Aquila city centre), then catch a TUA bus to Calascio (check out the TUA website)
Lake Campotosto (Lago Campotosto)

Marmore Waterfalls (Cascata delle Marmore)
 Marmore waterfalls are a man-made waterfall created in ancient times by Romans. Its total height is 165 m (541 feet), making it the tallest man-made waterfall in the world. Its source is a portion of the waters of river Velino (the rest of the river flows into a hydroelectric power plant), after flowing through Piediluco Lake near the community of Marmore. It pours into the valley below formed by the river Nera. Its flow is turned on and off based on a specific schedule, to satisfy the needs of tourists and the power company alike. Tourists try to be there the moment the gates are opened to see the powerful rush of water.
Marmore waterfalls are a man-made waterfall created in ancient times by Romans. Its total height is 165 m (541 feet), making it the tallest man-made waterfall in the world. Its source is a portion of the waters of river Velino (the rest of the river flows into a hydroelectric power plant), after flowing through Piediluco Lake near the community of Marmore. It pours into the valley below formed by the river Nera. Its flow is turned on and off based on a specific schedule, to satisfy the needs of tourists and the power company alike. Tourists try to be there the moment the gates are opened to see the powerful rush of water.
How to get there: catch a train from L'Aquila to Terni (a town in the nearby region called Umbria), then board a special bus called "Marmore link" which will take you from the Terni train station to the waterfalls in 20 minutes.
Adapted from Wikipedia
Gran Sasso National Laboratory

The Gran Sasso National Laboratory is one of the four INFN laboratories. It is the largest underground laboratory in the world for experiments in particle physics, particle astrophysics and nuclear astrophysics. It is used as a worldwide facility by scientists, presently over 900 in number, from 29 different countries, working at about 15 experiments in their different phases. It is located between the towns of L'Aquila and Teramo, about 120 km from Rome. Go to www.lngs.infn.it for more details and guided tours.
Beaches on the Adriatic coast

Other popular places are Alba Adriatica, Pineto, Pescara and Vasto. Pescara is by the way Abruzzo's largest city, with lots of shops, clubs and great nightlife, too. Just get to the main train station (Pescara Centrale, 2 hours away from L'Aquila, change trains in Sulmona; or just get there by TUA/ARPA bus). Outside the train station, you'll find yourself in the city centre with lots to do and see on the promenade that will take you right to the beach!
Sporting facilities
CANADA' Fitness Club [link]
WHERE. Coppito, campus of the Math Dept., just 2 minutes walking distance from our teaching buildings. MAP
DETAILS. Access to the area with weights machines ("sala pesi") costs only 25 euros/month (the average fare in other gyms is 40 euros) - a free trial pass is usually available. You can join extra courses like pilates, yoga, zumba, fitbox, and body pump, as well as reserve the outdoor fields. Check timetables and fares from the url.
CUS - Centro Universitario Sportivo [link]
WHERE. Statale 17 Bis (aka "Centi Colella", on the way from L'Aquilone Shopping Centre towards the My Suites Hotel - around 20 minutes walking distance from our department, but mind the traffic! Or just get on an AMA bus no. 2 or 19 from our department)
DETAILS. Large university sports centre with several halls and rooms for most popular sports (fitness, spinning, judo, climbing etc.), including outdoor fields (football, volleyball, rugby, tennis, etc.). Reduced fees for university students.
Piscina Comunale L'Aquila [link]
WHERE. Viale Ovidio 3 - L'Aquila (city centre, close to the castle)
DETAILS. City pool offering reduced fees for university students.
Circolo Tennis L'Aquila [link]
WHERE. Viale Ovidio 1 - L'Aquila (city centre, close to the castle)
SKI Resorts
Campo Imperatore [link]
Campo Felice [link]
Ovindoli [link]
L'Aquila Rugby [link]
WHERE. Strada Statale 17 Ovest, Centi Colella, L'Aquila (opposite the main Post Office)
L'Aquila football (soccer) Team [link]
There are quite a few private gyms (and swimming pools too) across the city, just google "palestra l'aquila" or "piscina l'aquila"
Libraries
Library in Coppito
(biblioteca in Italian), ground floor, Coppito1 building, DISIM (Math Dept.)
Open: Mon-Thu: 8.30 am – 7 pm, Fri: 8.30 am - 2 pm
The first time you enter the library you will be asked to register. So, bring with you an ID document and your student card.
More details can be found here
Library in the Department of Humanities (downtown, old city centre, address: viale Nizza 14)
Opening hours:
Mon - Fri: 8.30 am - midnight!
Sat: 9 am - 5 pm
Sun: 3 pm - 8 pm
Study & Computer rooms
You can find study rooms in the Canadà centre, which is at 2 minutes' walk from the main teaching building (aka Coppito1), (Math Dept).
There you'll also find a bar, a gym and a computer room, too.
Click here to view a map
Click here for their Facebook page
Find your nearest open pharmacy
Doctor-on-call (Guardia medica)
Address: Ex ONPI, via Capo Croce 1 ("Torrione" neighbourhood).
Available Mon-Fri from 8pm till 8 am, and from 10 am on Saturday till 8 am on the following Monday.
Psychological support
How to get to L'Aquila
Rome Fiumicino
Rome Ciampino
Both airports are connected to L'Aquila by express coach service operated by Gaspari or Flixbus. Read the section below ("By Bus") for further information.
Additional coach services (operated by T.U.A. and Itabus) are available from the "Tiburtina train station" (Stazione Tiburtina) located in East Rome. But that means you'll have to first get on a train/bus/undeground from the airport to get to the "Tiburtina train station", which will take you one hour or so, at least. So, we strongly suggest you use the other option above, as those coaches will be departing right from inside the aiport parking area.
Lastly, be informed that a bunch of European cities are also connected to the Abruzzo Airport in Pescara, located at about 100 km to the east of L'Aquila.
Getting to campus
Our programmes are coordinated and hosted by D.I.S.I.M. (Department of Information Engineering, Computer Science, and Mathematics) located on the Coppito campus in via Vetoio - West L'Aquila.
The Coppito campus also hosts other faculties: biology, chemistry, physics and, most importantly, the main city hospital ("ospedale" in Italian). Keep that in mind whenever you ask for directions, as everybody knows where the main hospital (ospedale) is.
Then, the University of L'Aquila is made up of several other campuses spread over the whole city, each of which has its own focus and identity. To get an overview, check out this interactive map.
Bus routes
There are two bus terminals:
A small one in west L'Aquila (generally referred to as "Hotel Amiternum", "Motel Agip" by locals or "Strada Statale S.S. 17"), which is actually a stall, but it's the spot where most Flixbuses, Gaspari buses or others from Rome, Fiumicino airports and other nearby towns will stop (for both alighting and boarding).
The actual Terminal in east L'Aquila (aka "Collemaggio" by locals because of the nearby Basilica, or more officially "Lorenzo Natali"), close to the historical centre.
Both websites are only in Italian, but all you need to do is enter the word "ospedale" or "Università - Polo Coppito" or "L'Aquila Ospedale Università" in the search box (indirizzo di arrivo).
Number 1 or 2U buses are very likely the AMA buses you'll need most, as they connect our campus to the bus station at the My Suites Hotel (aka Hotel Amiternum), the "L'Aquilone" shopping centre, as well as the main bus station (known as Collemaggio or Terminal) in the old city centre.
As bus routes are not available on Google Maps yet, we recommend